Basic & Econometrics - ARCH and GARCH modeling
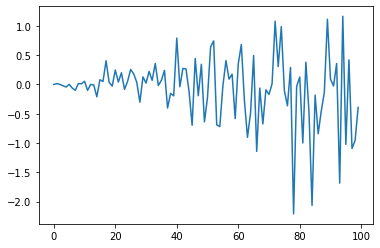
# create a simple white noise with increasing variance
from random import gauss
from random import seed
from matplotlib import pyplot
# seed pseudorandom number generator
seed(1)
# create dataset
data = [gauss(0, i*0.01) for i in range(0,100)]
# plot
pyplot.plot(data)
pyplot.show()
# check correlations of squared observations
from random import gauss
from random import seed
from matplotlib import pyplot
from statsmodels.graphics.tsaplots import plot_acf
# seed pseudorandom number generator
seed(1)
# create dataset
data = [gauss(0, i*0.01) for i in range(0,100)]
# square the dataset
squared_data = [x**2 for x in data]
# create acf plot
# plot_acf(squared_data)
# pyplot.show()
# split into train/test
n_test = 10
train, test = data[:-n_test], data[-n_test:]
# define model
model = arch_model(train, mean='Zero', vol='ARCH', p=15)
# fit model
model_fit = model.fit()
Iteration: 1, Func. Count: 18, Neg. LLF: 88229.21081826466
Iteration: 2, Func. Count: 36, Neg. LLF: 145.16342486790123
Iteration: 3, Func. Count: 54, Neg. LLF: 128.16575632743994
Iteration: 4, Func. Count: 72, Neg. LLF: 109.21743453644488
Iteration: 5, Func. Count: 90, Neg. LLF: 36.50573961108787
Iteration: 6, Func. Count: 108, Neg. LLF: 39.65738666780856
Iteration: 7, Func. Count: 126, Neg. LLF: 28.719725578734614
Iteration: 8, Func. Count: 143, Neg. LLF: 28.02027082653467
Iteration: 9, Func. Count: 161, Neg. LLF: 34.94722141328114
Iteration: 10, Func. Count: 180, Neg. LLF: 30.036240932703457
Iteration: 11, Func. Count: 198, Neg. LLF: 26.91679507719369
Iteration: 12, Func. Count: 216, Neg. LLF: 35.23299109213636
Iteration: 13, Func. Count: 235, Neg. LLF: 25.557783947221896
Iteration: 14, Func. Count: 253, Neg. LLF: 25.49687793461018
Iteration: 15, Func. Count: 271, Neg. LLF: 25.48620371888791
Iteration: 16, Func. Count: 289, Neg. LLF: 25.486110427773504
Iteration: 17, Func. Count: 307, Neg. LLF: 25.48214947994449
Iteration: 18, Func. Count: 324, Neg. LLF: 25.480673701601663
Iteration: 19, Func. Count: 341, Neg. LLF: 25.478363191699138
Iteration: 20, Func. Count: 358, Neg. LLF: 25.477639119935752
Iteration: 21, Func. Count: 375, Neg. LLF: 25.477510674022756
Iteration: 22, Func. Count: 392, Neg. LLF: 25.477507680721967
Iteration: 23, Func. Count: 408, Neg. LLF: 25.477507647045563
Optimization terminated successfully (Exit mode 0)
Current function value: 25.477507680721967
Iterations: 23
Function evaluations: 408
Gradient evaluations: 23
# forecast the test set
yhat = model_fit.forecast(horizon=n_test)
# example of ARCH model
from random import gauss
from random import seed
from matplotlib import pyplot
from arch import arch_model
# seed pseudorandom number generator
seed(1)
# create dataset
data = [gauss(0, i*0.01) for i in range(0,100)]
# split into train/test
n_test = 10
train, test = data[:-n_test], data[-n_test:]
# define model
model = arch_model(train, mean='Zero', vol='ARCH', p=15)
# fit model
model_fit = model.fit()
# forecast the test set
yhat = model_fit.forecast(horizon=n_test)
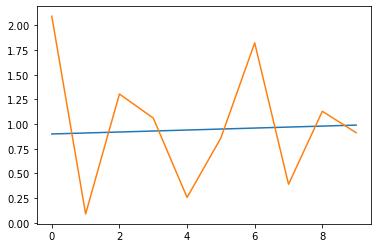
# plot the actual variance
var = [i*0.01 for i in range(0,100)]
pyplot.plot(var[-n_test:])
# plot forecast variance
pyplot.plot(yhat.variance.values[-1, :])
pyplot.show()
Iteration: 1, Func. Count: 18, Neg. LLF: 88229.21081826466
Iteration: 2, Func. Count: 36, Neg. LLF: 145.16342486790123
Iteration: 3, Func. Count: 54, Neg. LLF: 128.16575632743994
Iteration: 4, Func. Count: 72, Neg. LLF: 109.21743453644488
Iteration: 5, Func. Count: 90, Neg. LLF: 36.50573961108787
Iteration: 6, Func. Count: 108, Neg. LLF: 39.65738666780856
Iteration: 7, Func. Count: 126, Neg. LLF: 28.719725578734614
Iteration: 8, Func. Count: 143, Neg. LLF: 28.02027082653467
Iteration: 9, Func. Count: 161, Neg. LLF: 34.94722141328114
Iteration: 10, Func. Count: 180, Neg. LLF: 30.036240932703457
Iteration: 11, Func. Count: 198, Neg. LLF: 26.91679507719369
Iteration: 12, Func. Count: 216, Neg. LLF: 35.23299109213636
Iteration: 13, Func. Count: 235, Neg. LLF: 25.557783947221896
Iteration: 14, Func. Count: 253, Neg. LLF: 25.49687793461018
Iteration: 15, Func. Count: 271, Neg. LLF: 25.48620371888791
Iteration: 16, Func. Count: 289, Neg. LLF: 25.486110427773504
Iteration: 17, Func. Count: 307, Neg. LLF: 25.48214947994449
Iteration: 18, Func. Count: 324, Neg. LLF: 25.480673701601663
Iteration: 19, Func. Count: 341, Neg. LLF: 25.478363191699138
Iteration: 20, Func. Count: 358, Neg. LLF: 25.477639119935752
Iteration: 21, Func. Count: 375, Neg. LLF: 25.477510674022756
Iteration: 22, Func. Count: 392, Neg. LLF: 25.477507680721967
Iteration: 23, Func. Count: 408, Neg. LLF: 25.477507647045563
Optimization terminated successfully (Exit mode 0)
Current function value: 25.477507680721967
Iterations: 23
Function evaluations: 408
Gradient evaluations: 23
# define model
model = arch_model(train, mean='Zero', vol='GARCH', p=15, q=15)
# example of ARCH model
from random import gauss
from random import seed
from matplotlib import pyplot
from arch import arch_model
# seed pseudorandom number generator
seed(1)
# create dataset
data = [gauss(0, i*0.01) for i in range(0,100)]
# split into train/test
n_test = 10
train, test = data[:-n_test], data[-n_test:]
# define model
model = arch_model(train, mean='Zero', vol='GARCH', p=15, q=15)
# fit model
model_fit = model.fit()
# forecast the test set
yhat = model_fit.forecast(horizon=n_test)
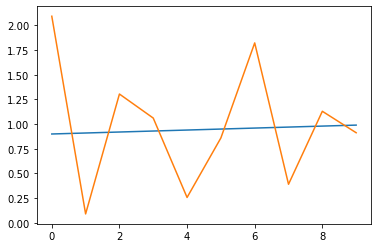
# plot the actual variance
var = [i*0.01 for i in range(0,100)]
pyplot.plot(var[-n_test:])
# plot forecast variance
pyplot.plot(yhat.variance.values[-1, :])
pyplot.show()
Iteration: 1, Func. Count: 33, Neg. LLF: 134.2317665883839
Iteration: 2, Func. Count: 70, Neg. LLF: 95219.42875514245
Iteration: 3, Func. Count: 103, Neg. LLF: 544.0651713801462
Iteration: 4, Func. Count: 136, Neg. LLF: 359.82260287255474
Iteration: 5, Func. Count: 169, Neg. LLF: 120.68468720344026
Iteration: 6, Func. Count: 202, Neg. LLF: 57.67993058484209
Iteration: 7, Func. Count: 235, Neg. LLF: 37.233844550362896
Iteration: 8, Func. Count: 268, Neg. LLF: 44.284908834009805
Iteration: 9, Func. Count: 301, Neg. LLF: 30.95579466733611
Iteration: 10, Func. Count: 334, Neg. LLF: 26.957522627026123
Iteration: 11, Func. Count: 366, Neg. LLF: 31.357987963939777
Iteration: 12, Func. Count: 400, Neg. LLF: 30.01446554259058
Iteration: 13, Func. Count: 433, Neg. LLF: 28.46108471907541
Iteration: 14, Func. Count: 466, Neg. LLF: 27.699881529397864
Iteration: 15, Func. Count: 499, Neg. LLF: 26.904390959213814
Iteration: 16, Func. Count: 532, Neg. LLF: 25.516070459707
Iteration: 17, Func. Count: 564, Neg. LLF: 25.510906607562323
Iteration: 18, Func. Count: 597, Neg. LLF: 25.783794390675624
Iteration: 19, Func. Count: 630, Neg. LLF: 25.492112073166872
Iteration: 20, Func. Count: 662, Neg. LLF: 25.485420508388895
Iteration: 21, Func. Count: 694, Neg. LLF: 25.479683744952947
Iteration: 22, Func. Count: 726, Neg. LLF: 25.477822001084277
Iteration: 23, Func. Count: 758, Neg. LLF: 25.477526070128754
Iteration: 24, Func. Count: 790, Neg. LLF: 25.477511628643917
Iteration: 25, Func. Count: 822, Neg. LLF: 25.47750785312727
Iteration: 26, Func. Count: 853, Neg. LLF: 25.47750781611067
Optimization terminated successfully (Exit mode 0)
Current function value: 25.47750785312727
Iterations: 26
Function evaluations: 853
Gradient evaluations: 26
print(model_fit.summary())
Zero Mean - GARCH Model Results
==============================================================================
Dep. Variable: y R-squared: 0.000
Mean Model: Zero Mean Adj. R-squared: 0.011
Vol Model: GARCH Log-Likelihood: -25.4775
Distribution: Normal AIC: 112.955
Method: Maximum Likelihood BIC: 190.449
No. Observations: 90
Date: Mon, Feb 15 2021 Df Residuals: 59
Time: 18:01:53 Df Model: 31
Volatility Model
========================================================================
coef std err t P>|t| 95.0% Conf. Int.
------------------------------------------------------------------------
omega 3.5755e-03 0.163 2.199e-02 0.982 [ -0.315, 0.322]
alpha[1] 0.0000 0.280 0.000 1.000 [ -0.549, 0.549]
alpha[2] 2.8289e-03 0.485 5.836e-03 0.995 [ -0.947, 0.953]
alpha[3] 0.3414 0.413 0.826 0.409 [ -0.469, 1.152]
alpha[4] 0.0000 1.238 0.000 1.000 [ -2.426, 2.426]
alpha[5] 0.0457 0.897 5.101e-02 0.959 [ -1.712, 1.803]
alpha[6] 0.1730 1.134 0.153 0.879 [ -2.050, 2.396]
alpha[7] 0.0000 1.307 0.000 1.000 [ -2.562, 2.562]
alpha[8] 0.1719 0.552 0.311 0.756 [ -0.910, 1.254]
alpha[9] 0.0109 1.844 5.901e-03 0.995 [ -3.603, 3.624]
alpha[10] 0.0000 1.810 0.000 1.000 [ -3.548, 3.548]
alpha[11] 0.0000 0.631 0.000 1.000 [ -1.237, 1.237]
alpha[12] 0.2542 2.076 0.122 0.903 [ -3.815, 4.324]
alpha[13] 0.0000 2.932 0.000 1.000 [ -5.746, 5.746]
alpha[14] 0.0000 1.103 0.000 1.000 [ -2.161, 2.161]
alpha[15] 0.0000 0.773 0.000 1.000 [ -1.514, 1.514]
beta[1] 0.0000 3.707 0.000 1.000 [ -7.266, 7.266]
beta[2] 0.0000 3.724 0.000 1.000 [ -7.300, 7.300]
beta[3] 0.0000 1.360 0.000 1.000 [ -2.665, 2.665]
beta[4] 0.0000 2.043 0.000 1.000 [ -4.004, 4.004]
beta[5] 0.0000 2.186 0.000 1.000 [ -4.285, 4.285]
beta[6] 0.0000 4.237 0.000 1.000 [ -8.305, 8.305]
beta[7] 0.0000 2.941 0.000 1.000 [ -5.765, 5.765]
beta[8] 0.0000 2.371 0.000 1.000 [ -4.647, 4.647]
beta[9] 0.0000 0.921 0.000 1.000 [ -1.806, 1.806]
beta[10] 0.0000 2.166 0.000 1.000 [ -4.245, 4.245]
beta[11] 0.0000 2.381 0.000 1.000 [ -4.668, 4.668]
beta[12] 0.0000 3.735 0.000 1.000 [ -7.321, 7.321]
beta[13] 0.0000 1.904 0.000 1.000 [ -3.732, 3.732]
beta[14] 0.0000 3.439 0.000 1.000 [ -6.739, 6.739]
beta[15] 0.0000 0.499 0.000 1.000 [ -0.978, 0.978]
========================================================================
Covariance estimator: robust
import pandas as pd
df = pd.DataFrame(data)
from tqdm import tqdm
tqdm.pandas()
/Users/ida/opt/anaconda3/lib/python3.8/site-packages/tqdm/std.py:697: FutureWarning: The Panel class is removed from pandas. Accessing it from the top-level namespace will also be removed in the next version
from pandas import Panel
df['test'] = df.progress_apply(lambda row: 1)
100%|██████████| 1/1 [00:00<00:00, 319.37it/s]
