Causal Inference - Instrumental Variables & Regression Discontinuity
def fn_tauhat_means(Yt,Yc):
nt = len(Yt)
nc = len(Yc)
tauhat = np.mean(Yt)-np.mean(Yc)
se_tauhat = (np.var(Yt,ddof=1)/nt+np.var(Yc,ddof=1)/nc)**(1/2)
return (tauhat,se_tauhat)
def fn_bias_rmse_size(theta0,thetahat,se_thetahat,cval = 1.96):
b = thetahat - theta0
bias = np.mean(b)
rmse = np.sqrt(np.mean(b**2))
tval = b/se_thetahat
size = np.mean(1*(np.abs(tval)>cval))
# note size calculated at true parameter value
return (bias,rmse,size)
def fn_run_experiments(tau,Nrange,p,p0,corr,conf,flagX=False):
n_values = []
tauhats = []
sehats = []
lb = []
ub = []
for N in tqdm(Nrange):
n_values = n_values + [N]
if flagX==False:
Yexp,T = fn_generate_data(tau,N,p,p0,corr,conf,flagX)
Yt = Yexp[np.where(T==1)[0],:]
Yc = Yexp[np.where(T==0)[0],:]
tauhat,se_tauhat = fn_tauhat_means(Yt,Yc)
elif flagX==1:
# use the right covariates in regression
Yexp,T,X = fn_generate_data(tau,N,p,p0,corr,conf,flagX)
Xobs = X[:,:p0]
covars = np.concatenate([T,Xobs],axis = 1)
mod = sm.OLS(Yexp,covars)
res = mod.fit()
tauhat = res.params[0]
se_tauhat = res.HC1_se[0]
elif flagX==2:
# use some of the right covariates and some "wrong" ones
Yexp,T,X = fn_generate_data(tau,N,p,p0,corr,conf,flagX)
Xobs1 = X[:,:np.int(p0/2)]
Xobs2 = X[:,-np.int(p0/2):]
covars = np.concatenate([T,Xobs1,Xobs2],axis = 1)
mod = sm.OLS(Yexp,covars)
res = mod.fit()
tauhat = res.params[0]
se_tauhat = res.HC1_se[0]
tauhats = tauhats + [tauhat]
sehats = sehats + [se_tauhat]
lb = lb + [tauhat-1.96*se_tauhat]
ub = ub + [tauhat+1.96*se_tauhat]
return (n_values,tauhats,sehats,lb,ub)
def fn_plot_with_ci(n_values,tauhats,tau,lb,ub,caption):
fig = plt.figure(figsize = (10,6))
plt.plot(n_values,tauhats,label = '$\hat{\\tau}$')
plt.xlabel('N')
plt.ylabel('$\hat{\\tau}$')
plt.axhline(y=tau, color='r', linestyle='-',linewidth=1,
label='True $\\tau$={}'.format(tau))
plt.title('{}'.format(caption))
plt.fill_between(n_values, lb, ub,
alpha=0.5, edgecolor='#FF9848', facecolor='#FF9848',label = '95% CI')
plt.legend()
Inspired by https://github.com/TeconomicsBlog/notebooks/blob/master/PrincipledInstrumentSelection.ipynb
def fn_generate_cov(dim):
acc = []
for i in range(dim):
row = np.ones((1,dim)) * corr
row[0][i] = 1
acc.append(row)
return np.concatenate(acc,axis=0)
def fn_generate_multnorm(nobs,corr,nvar):
mu = np.zeros(nvar)
std = (np.abs(np.random.normal(loc = 1, scale = .5,size = (nvar,1))))**(1/2)
# generate random normal distribution
acc = []
for i in range(nvar):
acc.append(np.reshape(np.random.normal(mu[i],std[i],nobs),(nobs,-1)))
normvars = np.concatenate(acc,axis=1)
cov = fn_generate_cov(nvar)
C = np.linalg.cholesky(cov)
Y = np.transpose(np.dot(C,np.transpose(normvars)))
# return (Y,np.round(np.corrcoef(Y,rowvar=False),2))
return Y
def fn_generate_data(tau,N,p,p0,corr,conf = True,flagX = False):
"""
p0(int): number of covariates with nonzero coefficients
"""
nvar = p+2 # 1 confounder and variable for randomizing treatment
corr = 0.5 # correlation for multivariate normal
if conf==False:
conf_mult = 0 # remove confounder from outcome
allX = fn_generate_multnorm(N,corr,nvar)
W0 = allX[:,0].reshape([N,1]) # variable for RDD assignment
C = allX[:,1].reshape([N,1]) # confounder
X = allX[:,2:] # observed covariates
# Make T a function of the W0's and unobservable (for RDD)
W = W0 + 0.5*C + 3*X[:,0]-6*X[:,1]
# assign treatment based on threshold along W
T = 1*(W>0)
T = fn_randomize_treatment(N) # choose treated units
err = np.random.normal(0,1,[N,1])
beta0 = np.random.normal(5,5,[p,1])
beta0[p0:p] = 0 # sparse model
Yab = tau*T+X@beta0+conf_mult*0.6*C+err
if flagX==False:
return (Yab,T)
else:
return (Yab,T,X)
# regression discontinuity
# W = W0 + 0.5*C+3*X[:,80].reshape([N,1])-6*X[:,81].reshape([N,1])
# treated = 1*(W>0)
# Yrdd = 1.2* treated - 4*W + X@beta0 +0.6*C+err
p = 10
p0 = 5
nvar = p+2 # 1 confounder and variable for randomizing treatment
tau = 1.2
corr = .5
N = 100
allX = fn_generate_multnorm(N,corr,nvar)
W0 = allX[:,0].reshape([N,1]) # variable for RDD assignment
C = allX[:,1].reshape([N,1]) # confounder
X = allX[:,2:] # observed covariates
# Make T a function of the W0's and unobservable (for RDD)
W = W0 + 0.5*C + 3*X[:,0].reshape([N,1])-6*X[:,1].reshape([N,1])
# assign treatment based on threshold along W
T = 1*(W>0)
err = np.random.normal(0,1,[N,1])
beta0 = np.random.normal(5,5,[p,1])
beta0[p0:p] = 0 # sparse model
Yrdd = tau*T - 4*W+X@beta0+0.6*C+err
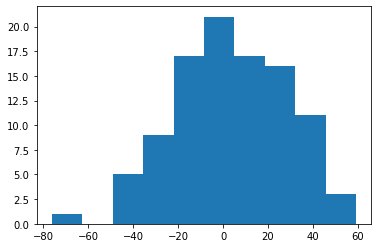
plt.hist(Yrdd)
(array([ 1., 0., 5., 9., 17., 21., 17., 16., 11., 3.]),
array([-76.21997922, -62.67705372, -49.13412822, -35.59120272,
-22.04827722, -8.50535172, 5.03757378, 18.58049928,
32.12342478, 45.66635028, 59.20927578]),
<BarContainer object of 10 artists>)
import pandas as pd
import numpy as np
import random
import statsmodels.api as sm
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedKFold
from sklearn.linear_model import Lasso
from sklearn.feature_selection import SelectFromModel
import matplotlib.pyplot as plt
from tqdm import tqdm
import statsmodels.api as sm
import itertools
from linearmodels import IV2SLS, IVLIML, IVGMM, IVGMMCUE
import copy
random.seed(10)
N = 1000
tau = 2
weak = np.random.normal(0,1,[N,1])
good = np.random.normal(0,1,[N,1])
correl = np.random.normal(0,1,[N,1]) # not exognous instrument
C = 3*correl + np.random.normal(0,1,[N,1])
X = -.00001 * np.round(weak) + 2.5 * correl + 2.5 * good + .5 * C + np.random.normal(0,1,[N,1])
Y = tau * X + 1.1 * C + np.random.normal(0,1,[N,1])
df = pd.DataFrame({'Y':Y[:,0],'X':X[:,0],'correl':correl[:,0],'good':good[:,0],'weak':weak[:,0]},index = None)
df.head()
| Y | X | correl | good | weak | |
|---|---|---|---|---|---|
| 0 | -12.972424 | -6.012842 | -0.588808 | -1.657263 | 0.550849 |
| 1 | 23.654806 | 8.116217 | 2.378486 | -0.486845 | -0.912524 |
| 2 | 5.926820 | 1.860624 | 0.441214 | -0.265508 | -1.396208 |
| 3 | -37.769825 | -15.705979 | -2.176071 | -1.956658 | -0.322946 |
| 4 | 17.074535 | 5.607653 | 1.817937 | -0.515070 | -2.358285 |
Naive regression without an instrument
mod = sm.OLS(Y,X)
res = mod.fit()
print(res.summary())
OLS Regression Results
=======================================================================================
Dep. Variable: y R-squared (uncentered): 0.969
Model: OLS Adj. R-squared (uncentered): 0.969
Method: Least Squares F-statistic: 3.135e+04
Date: Fri, 05 Feb 2021 Prob (F-statistic): 0.00
Time: 10:33:19 Log-Likelihood: -2229.1
No. Observations: 1000 AIC: 4460.
Df Residuals: 999 BIC: 4465.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
x1 2.5826 0.015 177.055 0.000 2.554 2.611
==============================================================================
Omnibus: 1.961 Durbin-Watson: 2.015
Prob(Omnibus): 0.375 Jarque-Bera (JB): 1.906
Skew: -0.046 Prob(JB): 0.386
Kurtosis: 3.193 Cond. No. 1.00
==============================================================================
Notes:
[1] R² is computed without centering (uncentered) since the model does not contain a constant.
[2] Standard Errors assume that the covariance matrix of the errors is correctly specified.
estDict = {} # store estimates
estDict['no_instrument'] = (float(res.params),float(res.HC0_se))
estDict
{'no_instrument': (2.582590351934214, 0.014621943546545573)}
We can also use the IV2SLS estimator with no instruments
ivmod = IV2SLS(df.Y, exog = df.X, endog = None, instruments = None)
res_2sls = ivmod.fit()
print(res_2sls.summary)
OLS Estimation Summary
==============================================================================
Dep. Variable: Y R-squared: 0.9689
Estimator: OLS Adj. R-squared: 0.9688
No. Observations: 1000 F-statistic: 3.059e+04
Date: Fri, Feb 12 2021 P-value (F-stat) 0.0000
Time: 15:09:54 Distribution: chi2(1)
Cov. Estimator: robust
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
X 2.6004 0.0149 174.91 0.0000 2.5713 2.6295
==============================================================================
/Users/ida/opt/anaconda3/lib/python3.8/site-packages/linearmodels/iv/data.py:25: FutureWarning: is_categorical is deprecated and will be removed in a future version. Use is_categorical_dtype instead
if is_categorical(s):
Fit using a good instrument (strong first stage and satisfies exclusion restriction)
ivmod = IV2SLS(df.Y, exog = None, endog = df.X, instruments = df.good)
res_2sls = ivmod.fit()
estDict['good_instrument'] = (float(res_2sls.params),float(res_2sls.std_errors))
print(res_2sls.summary)
IV-2SLS Estimation Summary
==============================================================================
Dep. Variable: Y R-squared: 0.9157
Estimator: IV-2SLS Adj. R-squared: 0.9156
No. Observations: 1000 F-statistic: 1645.8
Date: Fri, Feb 12 2021 P-value (F-stat) 0.0000
Time: 15:10:12 Distribution: chi2(1)
Cov. Estimator: robust
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
X 1.9911 0.0491 40.569 0.0000 1.8949 2.0873
==============================================================================
Endogenous: X
Instruments: good
Robust Covariance (Heteroskedastic)
Debiased: False
Fit using a weak instrument (satisfies exclusion restriction)
ivmod = IV2SLS(df.Y, exog = None, endog = df.X, instruments = df.weak)
res_2sls = ivmod.fit()
estDict['weak_instrument'] = (float(res_2sls.params),float(res_2sls.std_errors))
print(res_2sls.summary)
IV-2SLS Estimation Summary
==============================================================================
Dep. Variable: Y R-squared: 0.9623
Estimator: IV-2SLS Adj. R-squared: 0.9623
No. Observations: 1000 F-statistic: 17.369
Date: Fri, Feb 12 2021 P-value (F-stat) 0.0000
Time: 15:10:23 Distribution: chi2(1)
Cov. Estimator: robust
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
X 2.3870 0.5727 4.1677 0.0000 1.2644 3.5096
==============================================================================
Endogenous: X
Instruments: weak
Robust Covariance (Heteroskedastic)
Debiased: False
Fit using an instrument that doesn’t satisfy the exclusion restriction (but with a strong first stage)
Instrument correlated with unobservables
ivmod = IV2SLS(df.Y, exog = None, endog = df.X, instruments = df.correl)
res_2sls = ivmod.fit()
estDict['failed_excl'] = (float(res_2sls.params),float(res_2sls.std_errors))
print(res_2sls.summary)
IV-2SLS Estimation Summary
==============================================================================
Dep. Variable: Y R-squared: 0.9594
Estimator: IV-2SLS Adj. R-squared: 0.9594
No. Observations: 1000 F-statistic: 1.955e+04
Date: Fri, Feb 12 2021 P-value (F-stat) 0.0000
Time: 15:10:58 Distribution: chi2(1)
Cov. Estimator: robust
Parameter Estimates
==============================================================================
Parameter Std. Err. T-stat P-value Lower CI Upper CI
------------------------------------------------------------------------------
X 2.8567 0.0204 139.83 0.0000 2.8166 2.8967
==============================================================================
Endogenous: X
Instruments: correl
Robust Covariance (Heteroskedastic)
Debiased: False
estimates = [tau] + list(i[0] for i in estDict.values())
bnds = [0] + list(1.96*i[1] for i in estDict.values())
x_pos = np.arange(len(estimates))
labels = ['true']+list(estDict.keys())
estDict
{'no_instrument': (2.582590351934214, 0.014621943546545573),
'good_instrument': (1.9910988436149428, 0.04907956766829856),
'weak_instrument': (2.3869998034148607, 0.5727440776150304),
'failed_excl': (2.8566552323095524, 0.02042983578194687)}
labels
['true', 'no_instrument', 'good_instrument', 'weak_instrument', 'failed_excl']
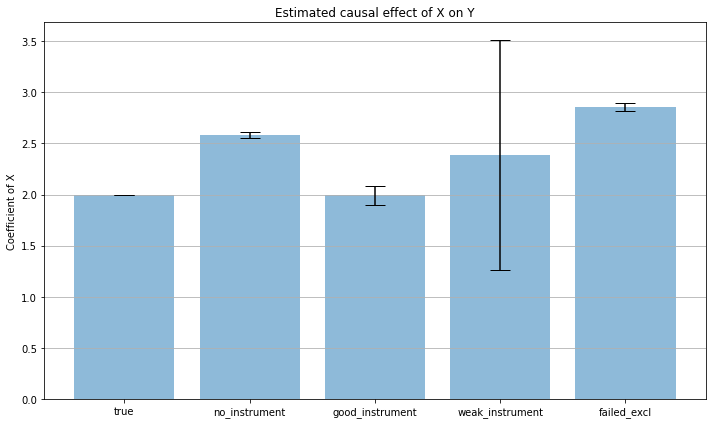
fig, ax = plt.subplots(figsize = (10,6))
ax.bar(x_pos, estimates, yerr=bnds, align='center', alpha=0.5, ecolor='black', capsize=10)
ax.set_ylabel('Coefficient of X')
ax.set_xticks(x_pos)
ax.set_xticklabels(labels)
ax.set_title('Estimated causal effect of X on Y')
ax.yaxis.grid(True)
# Save the figure and show
plt.tight_layout()
# plt.savefig('bar_plot_with_error_bars.png')
plt.show()
Monte Carlo example
R = 1000
N = 1000
tau = 2
l_weak = []
l_strong = []
for r in tqdm(range(R)):
# generate data
weak = np.random.normal(0,1,[N,1])
good = np.random.normal(0,1,[N,1])
correl = np.random.normal(0,1,[N,1]) # not exognous instrument
C = 3*correl + np.random.normal(0,1,[N,1])
X = -.00001 * np.round(weak) + 2.5 * correl + 2.5 * good + .5 * C + np.random.normal(0,1,[N,1])
Y = tau * X + 1.1 * C + np.random.normal(0,1,[N,1])
df = pd.DataFrame({'Y':Y[:,0],'X':X[:,0],'correl':correl[:,0],'good':good[:,0],'weak':weak[:,0]},index = None)
# estimation with weak instrument
ivmod = IV2SLS(df.Y, exog = None, endog = df.X, instruments = df.weak)
res_2sls = ivmod.fit()
l_weak = l_weak + [float(res_2sls.params)]
# estimation with strong instrument
ivmod = IV2SLS(df.Y, exog = None, endog = df.X, instruments = df.good)
res_2sls = ivmod.fit()
l_strong = l_strong + [float(res_2sls.params)]
100%|██████████| 1000/1000 [00:15<00:00, 66.64it/s]
plt.hist(l_strong)
(array([ 2., 9., 31., 100., 199., 250., 240., 124., 36., 9.]),
array([1.8199192 , 1.85138522, 1.88285125, 1.91431728, 1.9457833 ,
1.97724933, 2.00871536, 2.04018138, 2.07164741, 2.10311344,
2.13457946]),
<BarContainer object of 10 artists>)
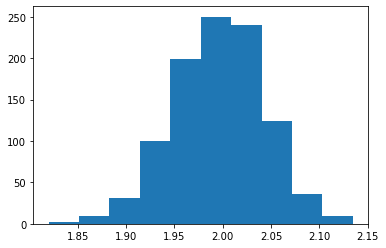
np.mean(l_strong)
1.9954114444265139
plt.hist(l_weak)
(array([ 1., 0., 0., 0., 0., 0., 2., 2., 992., 3.]),
array([-707.42250818, -622.92534886, -538.42818953, -453.9310302 ,
-369.43387087, -284.93671155, -200.43955222, -115.94239289,
-31.44523356, 53.05192576, 137.54908509]),
<BarContainer object of 10 artists>)

np.mean(l_weak)
1.6715375931589938
np.quantile(l_weak, q = [.0001,.1, .3, .5, .9, .99])
array([-654.32232836, 0.96837213, 2.26251629, 2.58687549,
4.13499364, 12.34641333])
mylist = [1,2,3]
emptylist = []
for i in range(10):
emptylist = emptylist + [i]
emptylist
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
